遇到和你同一天生的人概率有多大？

　　出品：科普中国

　　制作：李瑞（大阪大学 ）

　　监制：中国科学院计算机信息中心

　　3月14是什么子？

　　是本的白人节，同时也是圆周率之（圆周率常用的近似值是3.14）。不仅如此，很多名人都出生在这一天，例如科学家爱因斯坦、篮球运动员史蒂芬库里等。

　　所以有人将这一天称为“诞生奇迹的子”。不过如果仅因为这些事都发生在同一天，或是有很多名人都在这一天出生，就将其称为“特殊的子”，未免太过感性。毕竟，两个人在同一天出生的概率可能你想象的要大很多。

　　来源：699pic

　　一个班级中，出现相同生的概率有多大？

　　假设某小学某个班级有学生40人，其中出现相同生（同月同）的概率有多大？

　　这其实是一个排列组合的问题。首先，假定同出生的情况确实存在，那么可能的组合除了最简单的一种——两个人出生在同一天，还会有很多种。不同期都存在生相同的情况，如两个人出生在3月14，两个人出生在4月13。可能同一天出生的人不止两个，例如3月14出生的人有三个。

　　这样考虑起来的话，还可能出现三个人出生在某一天，四个人出生在另外一天之类的复杂情况。如果想要列举每个可能的组合，再把概率相加，事实上几乎是不可能完成的任务。

　　不过，假如从反面进行思考，这个问题就会变得简单很多。

　　同一个班级有重复生和没有重复生这两个事件发生的概率相加为1，只要计算出没有出现生重复的概率，再用1减去这一概率就是我们想要的结论。

　　如此一来，我们可以将问题简化成一个40人的小学班级中没有任何两个（或者更多）人出生在同一天的概率。

　　来源：699pic

　　为了便利，我们假定先把所有人请到教室外面，然后再挨个把同学们叫回来，并在这一过程中计算新加入同学和之前同学的生都不相同的概率。

　　假设第一位进教室的同学生是3月14，我们请第二位同学进场，为了满足题目的要求，第二位同学的生可以是365天中除了3月14的的任何一天，与第一位同学生不相同的概率是364/365。（这里我们做了两个假定，第一是不考虑闰年的情况，第二是全年每天的出生率应该均等。）

　　请第三位同学入场，他的生不能和之前两位同学一样，那么现在概率就变成了（364/365）×（363/365），第一个括号是前两位同学生不相同的概率，第二个括号是第三位和前两位生不同的概率，相乘的结果就是三人生都不同的概率。四个人生不同的概率就是（364/365）×（363/365）×（362/365）……

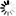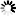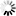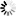
　　来源：作者自制

　　以此类推，一直计算到第40个人，再用1来减去算出的概率，就是我们想知道的问题答案，也就是40个人中出现生重复事件的概率。

　　最后得到的结果是89.1%。是不是预想的要大？

　　如果人数继续增加，这个概率还会急剧上升，50个人班级的这一概率是97.0%，60个人则达到99.4%，70个人已经是99.9%。换句话说，70个人的班级内没有任何生相同情况出现的概率小于千分之一。

　　来源：作者自制

　　小贴士：实际过程中我们无需傻傻地计算三四十次，计算机软件（简单的电子表格即可）能帮助我们完成这种重复繁琐的任务。

　　有一个非常经典的数学“悖论”叫做“生问题”：在一个房间最少要多少人，可以让其中两个人生相同的概率大于50%？

　　根据上面的计算方法，我们可以很容易地得到答案，23个人，相信这一数字大多人的直觉预估都要少。虽然称为“悖论”，但从引起逻辑矛盾的角度来说生问题并不是悖论，它被称作悖论只是因为这个数学事实与一般直觉相抵触而已。毕竟大多数人会认为，23人中有2人生相同的概率应该远远小于50%。

　　遇到和自己同一天生的人概率有多大？

　　说到这里，你可能会有一个疑惑：既然上面算出的概率都大得出乎意料，那为什么自己从小到大都没在班级中遇到和自己同天出生的人？

　　其实，如果你足够聪明，应该会意识到这是另外的一个命题——一个40人的班级中，出现和自己同天生人的概率是多少？

　　来源：699pic

　　我们还是用逐一请同学们进教室的思考方式解答问题。先计算40人班级中没有任何一个人跟自己生相同的概率，再用1减去这个值，就是我们需要的结果。

　　首先“我”进入教室，第二个进入教室的同学生和“我”不同的概率是364/365，第二、第三个同学生和“我”都不同的概率是（364/365）×（364/365），进入第四个同学时的答案是（364/365）×（364/365）×（364/365）……

　　以此类推，当进入第n个同学的时，概率是（364/365）的n-1次方。最后，我们再用1减去上面的结果，就是n个人的班级中，出现和自己同天生人的概率。计算结果如下：4个人的班级（0.8%）、23个人的班级（5.8%）、40个人的班级（10.1%）……

　　结果来看上一个问题更加符合我们的普遍认知。所以40个人的班级中，出现和自己生相同同学的概率是10.1%。

　　我们每个人从小到大都会加入很多班级，从以上的计算结果来看，假如从小到大任何一个班级中都没有生相同的人，那才是正的奇迹！我们以小学每个班60人，初中每个班70人，高中每个班50人，大学每个班30人进行计算，结果是小于一千万分之五，概率上来说已经到了彩票大奖的级别。

　　所以，一群人中出现生相同的概率就已经很多人的预想要大的多，更不用说全球几十亿人了。

　　当然，由于实际上每天的出生率并没有显著差别，全球70亿人中，某个期（注意是期不是具体的年份加期，如3月14，而非1985年3月14）对应的人口总数大约是2000万。如果再考虑历史上已经死去的人，那某天出生的人必然都是天文数字，其中的任何一天都有无数的名人出生或者故去。

　　这么说来，虽然我们希望每一天都是美好、特别、神奇的子，不过其实每一天都平凡而普通，任何一天都算不上是“奇迹之”。